Haii.... gaissss jumpa lagi...
lagi, lagi sama saya....
Sedikit saya akan sharing tentang
korelasi dan regulasi linier sederhana ....
Yukkk simak ya gaissss.....
Korelasi itu apa sih dan
contohnya seperti apa ??
Korelasi sederhana
merupakan suatu teknik statistik
yang digunakan untuk mengukur kekuatan hubungan dua variabel dan juga untuk
dapat mengetahui bentuk hubungan antara dua variabel tersebut dengan hasil yang
sifatnya kuantitatif.
jenis-jenis korelasi yang dapat
terjadi antara dua variable yaitu :
1.
Korelasi Positif
adalah korelasi dua variabel, apabila variabel independen (X) meningkat atau
turun maka variabel dependen (Y) cenderung untuk meningkat atau turun.
2.
Korelasi Negatif
adalah korelasi dua variabel, apabila variabel independen (X) meningkat atau
turun maka variabel dependen (Y) cenderung untuk turun atau meningkat.
3.
Tidak ada Korelasi
terjadi apabila kedua variabel X dan Y tidak menunjukan adanya hubungan.
4.
Korelasi Sempurna
adalah korelasi dari dua variabel yang benar-benar terjadi.
Rumus Koefisien Korelasi :
Interval yang menyatakan keeratan hubungan antar variabel yaitu :
Koefisien Determinasi
Untuk mengukur persentase
variabel Y yang dapat dijelaskan oleh variabel independen (X). Nilai koefisien
determinasi sebesar kuadrat dari koefisien korelasi.
Regresi Linier
Sederhana
Merupakan alat statistik
yang dipergunakan untuk mengetahui pengaruh antara satu atau beberapa variabel
terhadap satu buah variabel. Variabel yang mempengaruhi sering disebut variabel
bebas, variabel independen atau variabel penjelas.
Persamaan regresi sederhana
secara umum dituliskan sebagai berikut :
Y = Variabel dependen
X = Variabel independen
a = Konstanta
b = Koefisien regresi
dengan
Kesalahan Baku
Estimasi
Kesalahan baku atau selisih
taksir standar regresi adalah nilai menyatakan seberapa jauh menyimpangnya
nilai regresi tersebut terhadap nilai sebenarnya.
Rumus Kesalahan baku estimasi:
SX,Y = Kesalahan
baku
Y = Variabel dependen
t = Persamaan regresi
n = banyaknya sampel
Contoh 1.
Pak Budiman, manajer pemasaran
PT.ABC memiliki data harga jual dengan volume penjualan produknya selama 10
bulan, dan pak Budiman ingin mengamati hubungan, persentase variabel Y yang
dapat dijelaskan oleh variabel X, pengaruh dan kesalahan baku yang terjadi
antara dua variabel tersebut ?
Volume penjualan dan harga jual
produk PT.ABC dinyatakan dalam Tabel 1.
Penyelesaian:
Pada contoh 1, yang ditanyakan
adalah:
Kasus 1. Korelasi (hubungan
antara volume penjualan dengan harga jual)
Kasus 2. Persentase variabel Y
yang dapat dijelaskan oleh X (Koefisien determinasi)
Kasus 3. Regresi (pengaruh)
variabel independen terhadap variabel dependen Kasus
Kasus 4. Kesalahan baku estimasi
Jadi, terdapat 4 kasus yang harus
diselesaikan dalam contoh 1. Sebelum menyelesaikan kasus-kasus tersebut, kita
harus menentukan siapa yang menjadi variable X dan variabel Y.
Dengan mengingat kembali bahwa X adalah variabel independen
dan Y adalah variabel dependen. X adalah variabel yang
mempengaruhi . Sehingga dapat ditentukan bahwa X adalah harga
jual Y dan adalah volume penjualannya.
Setelah ditentukan siapa yang
menjadi variabel X dan Y, langkah selanjutnya adalah menghitung
nilai dari XY, X2 dan Y2 . Perhitungan
akan lebih mudah jika disajikan dalam bentuk Tabel 2.
Kasus 1. HUBUNGAN ANTARA VOLUME
PENJUALAN DAN HARGA JUAL
Untuk melihat hubungan antara X
dan Y maka dihitung nilai dari koefisien korelasi r dengan
menggunakan rumus yang sudah diberikan dan melihat nilai-nilai pada Tabel
2. Setelah semua data diinput, diperoleh nilai dari koefisien korelasi
sebagai berikut.
Koefisien korelasi sebesar -0,87
menunjukan hubungan linier negatif yang kuat artinya bila harga naik maka
volume penjualan akan turun.
Kasus 2. KOEFISIEN DETERMINASI
Persentase variabel Y yang dapat
dijelaskan variabel X, dengan menghitung koefisien determinasi yaitu dengan
mengkuadratkan koefisien korelasi
(-0,87)2 = 0,7569
Artinya kemampuan harga jual
barang dalam menjelaskan varians dari volume penjualan adalah sebesar 75,69%.
Berarti terdapat 24,31% (100% - 75,69%) varians volume penjualan yang
dijelaskan oleh faktor lain, misalnya kualitas barang.
Kasus 3. PENGARUH HARGA JUAL
TERHADAP VOLUME PENJUALAN
Untuk mengetahui pengaruh harga
jual terhadap volume penjualan (pengaruh X terhadap Y) maka
harus dilakukan pembuatan model regresi, . Sehingga terlebih dahulu
harus diitung nilai dari a dan b dengan menggunakan rumus
yang sudah dijelaskan.
Setelah
nilai a dan b diperoleh maka disubstitusikan pada model
regresinya, sehingga diperoleh:
Interprestasi dari model regresi.
Nilai b artinya jika
harga naik 1,00 (Rp.1000,00) maka volume penjualan akan turun sebesar 14,54
unit, begitu juga sebaliknya. Jika harga turun sebesar 1 (Rp. 1000,00) maka
volume penjualan naik sebesar 14,54 unit. Hal ini sesuai dengan analisis
mengenai korelasi antara harga jual dan volume penjualan, yang menyatakan bahwa
jika harga jual naik maka volume penjualan akan turun.
Kasus 4. KESALAHAN BAKU ESTIMASI
Selanjutnya, dilakukan perhitugan
mengenai kesalahan baku estimasi . Sebelum data dimasukkan pada rumus, baiknya
dilakukan perhitungan dengan menggunakan Tabel 3 untuk mempermudah perhitungan
kesalahan baku estimasinya.
Setelah tabel dibuat, selanjutnya
dimasukkan ke dalam rumus kesalahan baku estimasi yaitu:
Nilai dari kesalahan baku
estimasinya sebesar 2,73. Artinya jauhnya penyimpangan nilai regresi terhadap
nilai sebenarnya adalah sebesar 2,73.
Pengujian Hipotesis
Pengujian hipotesis dilakukan
jika terdapat seseorang yang mempunyai pendapat atau argumen dan ingin
dibuktikan kebenarannya. prosedur pengujian hipotesis tentang korelasi dan
regresi linier berganda, dapat diilustrasikan menggunakan skema berikut :
Pengujian Hipotesis
Tentang Koefisien Korelasi
Perumusan hipotesis yang
digunakan untuk korelasi adalah sebagai berikut :
Langkah-langkah Pengujian
Hipotesis :
1. Merumuskan bentuk hipotesis :
2. Menentukan nilai kesalahan = α,
setelah α diketahui kemudian mencari tα (jika satu arah)
atau t α/2 (jika dua arah) dari Tabel t (Lampiran 1)
dengan df = n - 2.
df = derajat
kebebasan.
3. Menghitung nilai dari t hitung
dengan rumus:
th = nilai t ℎitung
r = koefisien
korelasi
n = jumlah
sampel
4. Keputusan
Kriteria keputusan
dalam pengujian hipotesis korelasi adalah sebagai berikut :
Pengujian Hipotesis
Tentang Regresi
Perumusan hipotesis yang
digunakan untuk regresi adalah sebagai berikut :
Langkah-langkah Pengujian
Hipotesis :
1. Merumuskan bentuk hipotesis :
Ho : B = 0 Ha : B
< 0 Pengujian satu arah
Ha : B > 0
Pengujian satu arah
Ha : B ≠ 0 Pengujian
dua arah
2. Menentukan nilai kesalahan = α,
setelah α diketahui kemudian mencari tα (jika satu arah)
atau t α/2 (jika dua arah) dari Tabel t (Lampiran 1)
dengan df = n - 2.
df = derajat
kebebasan.
3. Menghitung nilai dari t hitung
dengan rumus:
Sb=
Kesalahan baku
SY,X =
Kesalahan baku estimasi
4. Keputusan
Kriteria keputusan
dalam pengujian hipotesis korelasi adalah sebagai berikut :
CONTOH 2
Seseorang berpendapat bahwa ada
hubungan dan pengaruh yang positif antara besarnya upah mingguan (puluhan
ribuan) dengan pengeluaran konsumsi (puluhan ribuan). Untuk itu diambil
sampel 5 orang karyawan sehingga diperoleh hasil sebagai berikut :
Ujilah pendapat tersebut dengan α
= 5%
Penyelesaian:
Pada contoh 2, kita harus
membuktikan bahwa argumen dari seseorang itu benar. Yaitu dengan menggunakan
pengujian hipotesis. Pengujian hipotesis yang akan dianalisis meliputi:
Kasus 1. Pengujian hipotesis
tentang korelasi.
Kasus 2. Pengujian hipotesis
tentang regresi.
Jadi, terdapat 2 kasus yang harus
diselesaikan dalam contoh 1. Sebelum menyelesaikan kasus-kasus tersebut, kita
harus menentukan siapa yang menjadi variabel X dan
variabel Y . Dengan mengingat kembali bahwa X adalah
variabel independen dan Y adalah variabel
dependen. X adalah variabel yang mempengaruhi Y . Sehingga
dapat ditentukan bahwa X adalah upah mingguan dan Y adalah
pengeluaran konsumsi.
Selanjutnya dihitung data-data
dan dicantumkan dalam Tabel 4.
Kasus 1. Pengujian
hipotesis tentang korelasi
1. Perumusan Hipotesis
Dari contoh 2, dapat
diketahui bahwa argumen dari seseorang itu adalah ada hubungan yang positif
antara besarnya upah mingguan dengan pengeluaran konsumsi. Sehingga untuk
hipotesis alternatif yang digunakan adalah Ha : p > 0
(X dan Y mempunyai hubungan positif)
Berdasarkan informasi
tersebut, kita dapat merumuskan hipotesisnya sebagai berikut.
2. Dari contoh 2 diketahui taraf
nyata yang ditentukan adalah α = 5% = 0,05. Selanjutnya akan ditentukan nilai
dari t tabel dengan menggunakan
tabel t pada Lampiran 1 dengan derajat kebebasannya adalah n – 2
= 5 – 2 = 3 . Sehingga diperoleh:
3. Untuk menghitung nilai ℎ terlebih
dahulu dihitung nilai dari koefisien korelasi. Diperoleh nilai sebagai
beriku :
Selanjutnya dihitung
nilai dari tℎ dengan mensubstitusikan semua
nilai yang sudah diperoleh. Sehingga
4. Keputusan
Dari perhitungan pada
poin 2 dan 3 diperoleh bahwa nlai dari t tabel =
2,35 dan nilai dari tℎ = 19, 382. Berdasarkan kriteria pengujian
hipotesis diambil keputusan bahwa H0 ditolak karena tℎ > ta.
Artinya ada hubungan
yang positif antara tingkat upah dengan pengeluaran konsumsi dengan
probabilitas penarikan keputusan bernilai benar sebesar 95%.
Kasus 2. Pengujian
hipotesis tentang regresi
1. Dari contoh 2, dapat diketahui
bahwa argumen dari seseorang itu adalah ada pengaruh yang positif antara
besarnya upah mingguan dengan pengeluaran konsumsi. Sehingga untuk hipotesis
alternatif yang digunakan adalah Ha : B > 0 (Ada pengaruh
positif X terhadap Y). Berdasarkan informasi tersebut, kita
dapat merumuskan hipotesisnya sebagai berikut :
2. Dari contoh 2 diketahui taraf
nyata yang ditentukan adalah α = 5% = 0,05. Selanjutnya akan ditentukan nilai
dari t tabel dengan menggunakan
tabel t pada Lampiran 1 dengan derajat kebebasannya adalah n – 2
= 5 – 2 = 3 . Sehingga diperoleh:
3. Untuk menghitung nilai tℎ terlebih dahulu dihitung nilai dari dan .
Diperoleh nilainya sebagai berikut :
Sehingga diperoleh
model regresinya sebagai berikut :
Selanjutnya akan
dihitung nilai kesalahan baku estimasi. Dengan memasukkan semua data yang ada
pada Tabel 5 untuk mempermudah perhitungan.
Semua data yang
diperoleh disubstitusikan ke rumus kesalahan baku estimasi, sehingga diperoleh:
Kemudian dilanjutkan
dengan perhitungan dari (X – X)2 yang disajikan dalam
Tabel 6.
Setelah semua nilai
diketahui, maka nilai-nilai tersebut disubstitusikan ke rumus , sehingga
diperoleh:
Kemudian dilanjutkan
menghitung untuk nilai tℎ, yaitu:
4. Keputusan
Dari perhitungan pada
poin 2 dan 3 diperoleh bahwa nlai dari t tabel =
2,35 dan nilai dari tℎ = 18,609. Berdasarkan kriteria pengujian
hipotesis diambil keputusan bahwa H0 ditolak karena tℎ >
ta .
Artinya ada hubungan
yang positif antara tingkat upah dengan pengeluaran konsumsi dengan
probabilitas penarikan keputusan bernilai benar sebesar 95%.
Sekian ya Gaissss... semoga
bermanfaat J








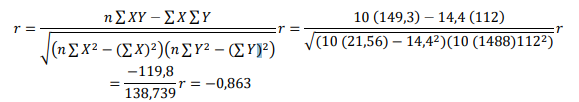






























Tidak ada komentar:
Posting Komentar