Jumpa lagi
dengan saya gaissss
Yang setiap
minggunya selalu berbagi materi tentang statistik....
Kali ini pun
saya akan melakukan
hal yang sama tetapi dengan judul “Distribusi
Sampling”
Apa itu yuk
simak ya gaissss
Distribusi
sampling adalah distribusi dari besaran-besaran statistik seperti rata-rata,
simpangan baku, proporsi yang mungkin muncul dari sampel-sampel.
Sampling yang baik adalah
sampling yang dapat menghemat biaya biaya dan waktu, serta menjaga keakuratan hasil-hasilnya.
Secara khusus teknik sampling berguna dalam Estimasi parameter populasi
(seperti mean populasi, varians populasi dll.)
Metoda
Penarikan Sampling ada 2 yaitu :
1.
Penarikan sampel probabilitas:
·
prosedur objektif: probabilitas
pemilihan diketahui terlebih dahulu untuk setiap elemen populasi.
·
setiap elemen populasi memiliki
probabilitas yang sama sebagai sampel.
·
metode pemilihan acak (random),
konsep matematik yang tepat , sehingga setiap elemen dalam populasi memiliki
peluang yang sama sebagai sampel.
2.
Penarikan sampel non probabilitas:
·
prosedur subjektif, kerangka
sampelnya tidak tersedia.
·
Setiap elemen populasi tidak
memiliki probabilitas yang sama sebagai sampel, dipilih berdasarkan
pertimbangan-pertimbangan pribadi.
PROBABILITY SAMPLING
1.
Sampling acak sederhana (simple
random sampling)
·
Baik (bukti empiris yang
dihasilkan), representative
·
Populasi terbatas: peluang acak
secara individual.
·
Populasi banyak dan berkelompok:
mengambil sejumlah kelompok yang ada, kemudian
pengambilan sampel acak dilakukan pada kelompok tersebut.
Sampling
acak berstrata disproporsional
Yaitu Bila populasi berstrata, tetapi kurang
proporsional.
Prinsip sampling
disproporsional adalah :
·
Semakin besar suatu strata,
semakin besar sampel
·
Semakin tinggi variabilitas di
dalam suatu sampel, semakin besar sampel
2.
Sampling
acak berstrata proporsional (proportioned stratified random sampling)
Subsample-subsampel acak sederhana ditarik dari setiap strata
yang kurang lebih sama dalam beberapa karakteristik.
a.
Sampling acak berstrata proporsional
Bila populasi mempunyai anggota/unsur tidak homogen dan
berstrata secara proporsional. Untuk suatu organisasi yang mempunyai pegawai
dengan latar belakang pendidikan berstrata, populasi pegawai itu berstrata.
3.
Metode sampling berkelompok (cluster sampling) yaitu :
§ Memilih
subpopulasi yang disebut klaster, setiap elemen kelompok dipilih sebagai
anggota sampel.
§ Untuk
objek dengan data sangat luas (penduduk Negara, provinsi) samplingnya
berdasarkan daerah populasi yang telah ditetapkan.
§ Kriteria
cluster bertolak belakang dengan apa yang digunakan dalam sampling berstrata.
§ Populasi
harus dibagi ke dalam kelompok-kelompok yang bersifat mutually exclusive,
selanjutnya dipilih secara acak sebagai sampel.
NON PROBABILITY
SAMPLING
·
Prosedur bersifat subjektif.
·
Probabilitas pemilihan elemen
populasi tidak dapat ditentukan.
·
Hemat waktu/biaya ( tidak perlu
kerangka sampling)
·
Hasilnya bisa bias dan
ketidakpastian.
·
Misalnya, dalam suatu penelitian
terhadap para pengunjung mal atau pusat-pusat, perbelanjaan.
a.
Sampling Sistematik
b.
Berdasarkan urutan anggota
populasi (populasi dibagi dengan ukuran sampel yang diperlukan (n) dan sampel
diperoleh dengan cara mengambil setiap subjek ke-n).
c.
Sampling Wilayah
d.
Sampling klaster dalam suatu
wilayah.
e.
Sampling Kemudahan
f.
Untuk mendapatkan informasi
dengan cepat, mudah dan murah.
g.
Sampling Pertimbangan
h.
Didasarkan pada kriteria-kriteria
tertentu.
i.
Sampling Kuota
j.
Bentuk lain sampling
pertimbangan, karakteristik-karakteristik tertentu yang relevan yang
menjelaskan dimensi-dimensi populasi.
Populasi terhingga dan tak tehingga
Populasi terhingga (finite
population) adalah populasi yang jumlah seluruh anggotanya tetap dan dapat
didaftar. Populasi tak terhingga (infinite population) memiliki anggota yang
banyaknya tak terhingga.
Distribusi Sampling Rata-Rata
Distribusi sampling
rata-rata merupakan distribusi normal, yang berbentuk lonceng, simetris dan
memiliki rata-rata dan deviasi standar.
Dalil Batas Memusat (The Central Limit Theorem)
Dalil yang menyatakan
bahwa untuk suatu populasi dengan rata-rata dan varian : distribusi sampling
rata-rata dari semua kemungkinan sampel berukuran n yang diambil dari populasi
akan terdistribusi secara normal dengan rata-rata sama dengan rata-rata populasi
dan deviasi standar , dengan deviasi standar populasi dibagi akar atau √ ,
dengan asumsi bahwa ukuran sampel cukup besar.
Jika ukuran sampel (n ) cukup besar, distribusi
rata-rata sampel akan mendekati normal, tidak peduli apakah populasinya terdistribusi
secara normal atau tidak, dengan
keterangan :
Tidak ada angka yang pasti
tentang “ukuran sampel yang cukup besar”, tetapi biasanya angka n > 30
dianggap cukup besar.
Distribusi Sampling Beda Rata-rata
Misalkan proporsi populasi
dinotasikan dengan dengan .
dimana
jumlah item proporsi
adalah jumlah seluruh
item.
Sebagai contoh, total
mahasiswa adalah 100 orang, jika 30 mahasiswa diantaranya merokok, proporsi
mahasiswa yang merokok adalah 30/100 atau 30%.
Misalkan populasi adalah N dan sampel adalah n, berarti kita telah memiliki p (proporsi sampel) sebanyak C(N,n)
. P yang dimaksud berjumlah sangat besar dan
membentuk distribusi normal dengan rata-rata
dan
deviasi standar
. Dimana
Distribusi Sampling Beda Proporsi
Misalkan populasi 1 adalah
N1 dan sampel 1
adalah n1 maka terdapat C (N1,n1)
dengan proporsi p1. Sedangkan populasi 2
adalah N2 dan sampel 2 adalah n1
maka terdapat C (N2,n2) dengan
proporsi p2 . Selisih dari p1 dan p2 membentuk distribusi
normal dengan rata-ratanya adalah
Berikut Contoh – Contoh soal Distribusi Sampling
Contoh 3
Berikut teknik pengambilan sampel.
Sekian gaisss, semoga bermanfaat J


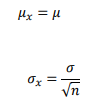














Tidak ada komentar:
Posting Komentar